Mercury was imaged very low in the sky. Around 22 degrees altitude.

You can see the strong dispersion between R, G, and B channels. This image was wavelet processed in registax and then up-sampled in Pixinsight by 4.8, and cropped. Using Registax to automatically determine the offsets, it comes up with 6 up in the red channel and -12 in the blue channel to get:

The native image resolution based on my imaging chain (1250 mm FL and 2.2 micron pixels, 0.0000022/1.25*180/pi*3600) is 0.36″.
Now rotate it to look good to get:

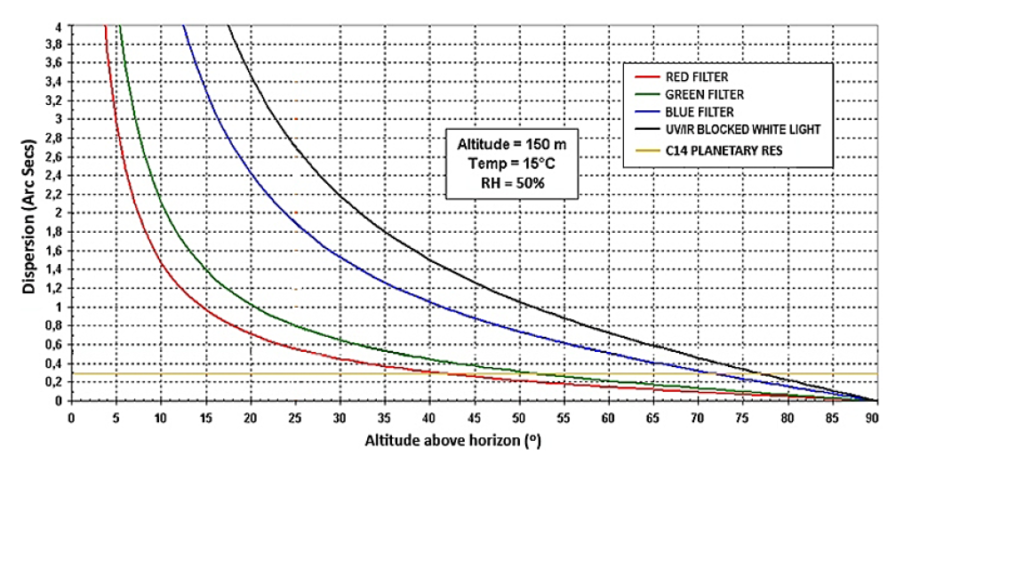
At 22 deg it says 0.65″ red, 1″ green, and 2.2″ blue, and 3.2″ across a white band.
According to the table the total dispersion across the band would be around 3.3 arc-seconds. Since I have about 0.075 arc-seconds per pixel (0.36/4.8) and the correction is 18 pixels total, that implies 1.35″ correction. This makes sense if you assume that you are moving the red and blue channels 1/2 the dispersion “bandwidth” to lay on top of the green.
This also implies that the image should be significantly wider at blue that red or green.

